Basic algorithm implementation
Optimized algorithm implementation
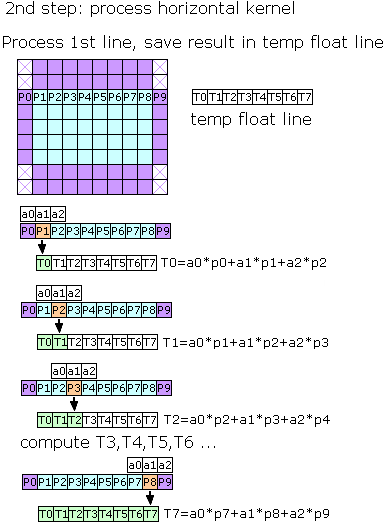
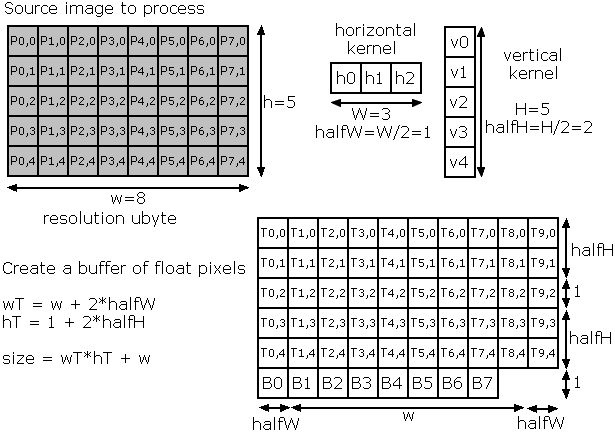
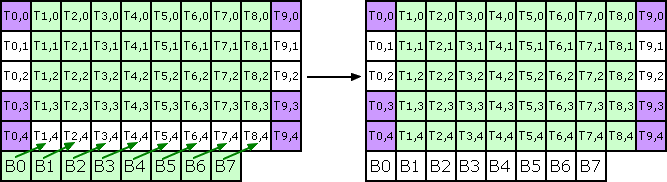
Process source image horizontal line
Point 1
-
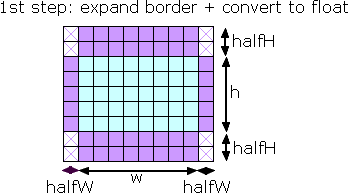
Copy source image converting to float
-
Fill border: black, white or nearest (copy)
-
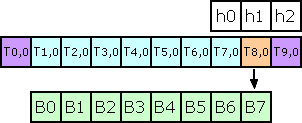
Process horizontal temp buffer line
B0 = h0*T0,0 + h1*T1,0 + h2*T2,0
B1 = h0*T0,1 + h1*T1,1 + h2*T2,1
Compute B2,B3...
B7 = h0*T7,1 + h1*T7,1 + h2*T7,1
-
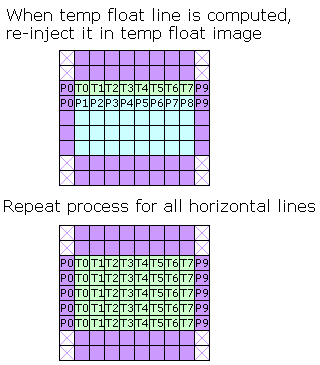
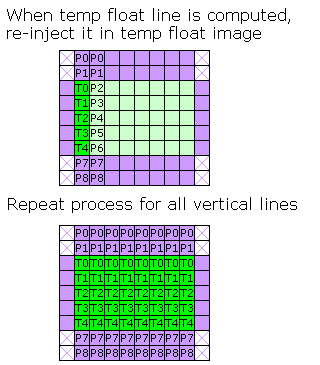
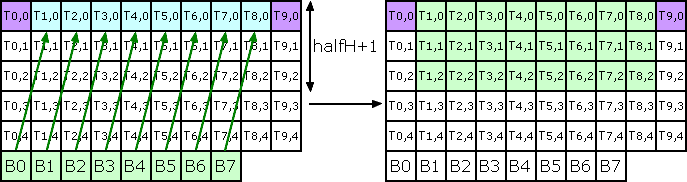
Re-inject temp line into halfH+1 line(s) from line 0 of temp buffer
-
For next halfH lines, process like as Point 1 but change lines
-
Re-inject temp line into next temp buffer line
-
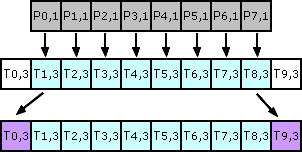
Compute next (last) temp horizontal line
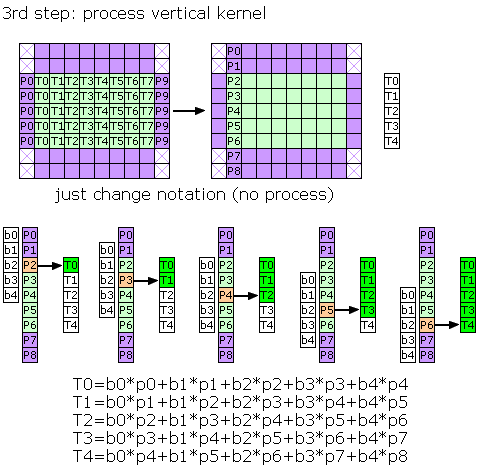
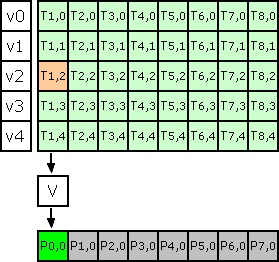
Now we can can apply vertical kernel for whole image first line.
Point2
compute V = v0*T1,0 + v1*T1,1 + v2*T1,2 + v3*T1,3 + v4*T1,4
clamp V on demand and convert back to ubyte into original image
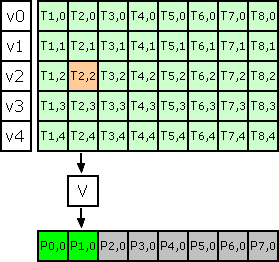
compute V = v0*T2,0 + v1*T2,1 + v2*T2,2 + v3*T2,3 + v4*T2,4
clamp V on demand and convert back to ubyte into original image
Compute P2,0, P3,0, P4,0 ....
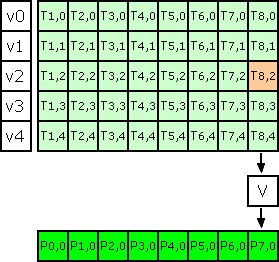
compute V = v0*T8,0 + v1*T8,1 + v2*T8,2 + v3*T8,3 + v4*T8,4
clamp V on demand and convert back to ubyte into original image
First line is now computed into original image.
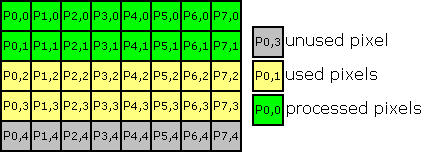
Process next lines
-
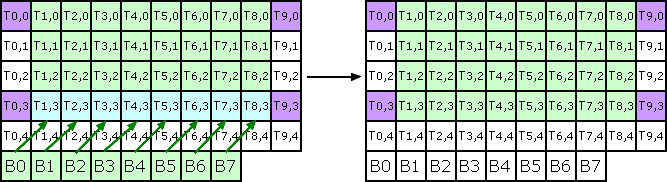
move buffer lines for bottom to top
Compute new temp line like in Point 1 but reading for P0,3 and writing into buffer last line (Tx,H-1).
Process buffer with vertical kernel like in Point2 but destination is original image line P0,1
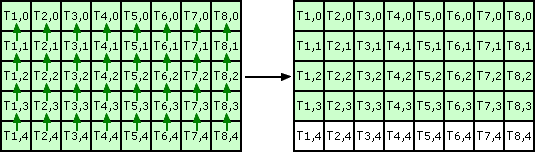
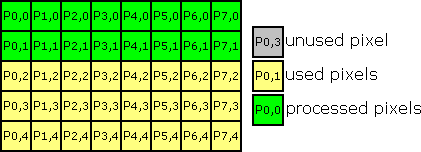
So we get:
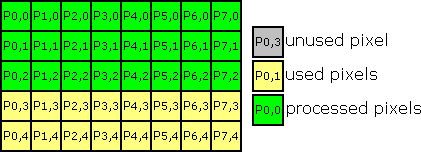
Process next line the same reading from P0,4
Writing to P0,2, so we get:
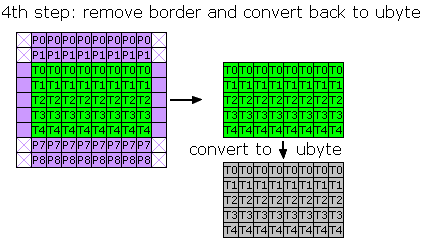
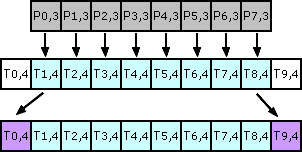
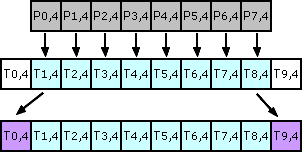
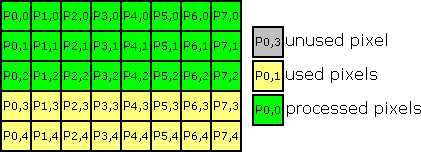
For last halfH lines process identically except that we won't fill last buffer line from image source.
So after shifting last temp buffer line is duplicated. We get:
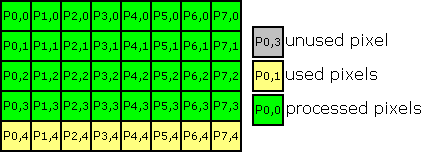
Now it's done :)